Implied volatility is the projected future volatility of a stock inferred from the prices of its options. The fair market price of a given option can be calculated based on five factors:
- The current price of the stock
- The current price of the option (typically calculated as the average of the best bid and ask prices for the option)
- The amount of time until expiration
- The risk-free rate of return (typically the Libor rate for that duration)
- The historical volatility of the stock
However, options rarely trade at their fair market price, which implies that those buying and selling the options expect the stock to trade at a different volatility from its historical volatility. When replacing this implied volatility into the option pricing model, the resulting price will match the option’s current market value.
The implied volatility measurements provided are calculated for calls, puts, and means using at-the-money (ATM) options for predefined durations. For the purposes of this data set, an ATM option is one whose strike price is the closing price as of the date of calculation, which may be rounded to two decimals, such as $12.34. The durations are all measured in calendar days.
For example, the 30-day call implied volatility provides the implied volatility of the ATM call for the stock with an expiration 30 calendar days from the measurement date. If the stock closed at $12.34 on that day, the option used would be the call with the strike at $12.34. The 30-day put implied volatility represents the implied volatility for the comparable put, and the 30-day mean is simply the average of the 30-day call and put values. The provided durations are 10, 20, 30, 60, 90, 120, 150, 180, 270, 360, 720, and 1080 calendar days.
As it is very uncommon for there to be options that precisely fit the strike and expiration requirements to fulfill these measurements, a multi-step process is employed to calculate the values.
- The implied volatility for each of the available options is calculated. If there are no ordinary dividends to be distributed over the remaining lifetime of a given option, the Black-Scholes model is employed. If there are ordinary dividends to be distributed, the system uses the Cox-Ross-Rubinstein binomial model. For long-range options, the system infers the likelihood of future dividends based on the current expectations for ordinary dividends over the next year.
- Once the implied volatility has been calculated for each option, the ATM option for that duration is calculated using linear interpolation of the two options straddling the ATM price. For example, if the ATM price is $102, the system may use the $100 and $105 strikes to calculate the theoretical $102 strike using a 3:2 weighted ratio (linear interpolation).
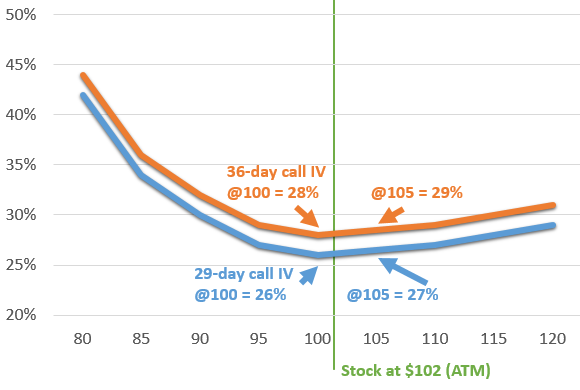
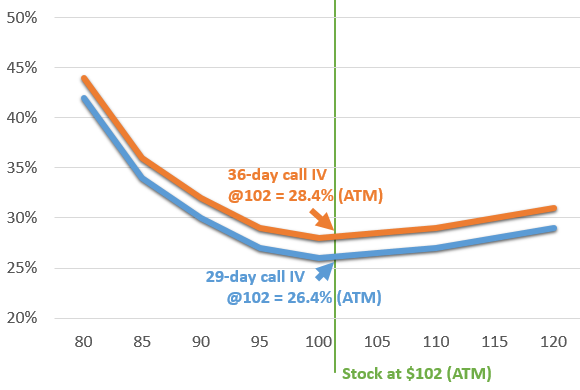
In the rare case where all options are above or below the ATM price, the implied volatility of the option closest to the money is used. Note that only call options are used to calculate call implied volatilities and only puts are used for put implied volatilities. - At this point, the system has the ATM implied volatilities for each actual expiration of the options available for the stock. To calculate the implied volatilities for the predefined durations, the system uses linear interpolation between the two expiration periods straddling the target expiration. For example, if the target duration is 30 days, the system may use the 29-day and 36-day ATM implied volatilities at a ratio of 6:1 (linear interpolation) to calculate the theoretical 30-day implied volatility.

- The “mean” implied volatilities are calculated by averaging the call and put volatilities using the same strikes and terms. When implied volatilities are used, it should be assumed these are mean volatilities unless otherwise specified.